Moduł 6 - "Gra logiczna - zgadywanie liczby"
Materiały stworzone przez Ośrodek Edukacji Informatycznej i Zastosowań Komputerów w Warszawie w ramach Programu „Mistrzowie Kodowania” finansowanego przez Samsung Electronics Polska, objęte licencją CC-BY-SA „Uznanie autorstwa – Na tych samych warunkach 3.0 Polska”
Spis treści
- 1 Informacje
- 2 Etapy realizacji
- 2.1 Omówienie rozwiązania zadania dodatkowego z modułu V
- 2.2 Zaprojektowanie gry polegającej na zgadywaniu liczby, którą wylosował komputer
- 2.3 Implementacja gry logicznej „Zgadywanie liczby”
- 2.4 Wprowadzenie drugiego duszka do gry i komunikacji między ich skryptami
- 2.5 Wprowadzenie licznika pytań
- 2.6 Propozycja zadania dodatkowego do samodzielnej realizacji przez uczniów
Informacje
Cele
Cele ogólne:
- przypomnienie i utrwalenie poznanych wcześniej poleceń i konstrukcji języka Scratch,
- wprowadzenie algorytmu przeszukiwania binarnego,
- opracowanie projektu prostej gry logicznej,
- jej implementacja w środowisku Scratch.
Cele szczegółowe:
- uczeń rozumie i potrafi stosować odpowiednie instrukcje strukturalne, w tym iterację warunkową,
- uczeń rozumie pojęcie zmiennej i potrafi je wykorzystać w programie,
- uczeń rozumie i potrafi posługiwać się komunikatami i programować reakcje na otrzymanie komunikatu,
- uczeń potrafi implementować prostą grę logiczną w środowisku Scratch,
- uczeń posługuje się algorytmem przeszukiwania binarnego.
Etapy realizacji
Omówienie rozwiązania zadania dodatkowego z modułu V
Czas na realizację tej części: ok. 10 minut
Na początku zajęć należy przypomnieć, co miało zostać przygotowane przez uczniów między zajęciami. Zapraszamy chętnego ucznia do zaprezentowania swojego rozwiązania. Dyskutujemy z uczniami, czy ktoś miał inny sposób rozwiązania. Omawiamy rozwiązania (chwaląc każde poprawne rozwiązania poszczególnych zadań).
Jeśli nie było zadań domowych, to zaczynamy od powtórzenia najważniejszych zagadnień z poprzedniego modułu. Pytamy także, o wątpliwości do ew. własnych projektów uczniów. Jeśli ktoś chce się czymś pochwalić – pozwólmy mu na to.
Zaprojektowanie gry polegającej na zgadywaniu liczby, którą wylosował komputer
Czas na realizację tej części: ok. 20 minut
Na początku zajęć przedstawiamy koncepcję projektu, który chcemy opracować podczas zajęć. Wspólnie z uczniami zastanawiamy się, jak mogłaby działać gra polegająca na zgadywaniu liczby, wylosowanej przez komputer. Zastanawiamy się nad tym, jak powinien reagować program na udzielenie poprawnej i błędnej odpowiedzi. Jak odpowiedź, udzielona przez program może naprowadzić gracza na właściwy wynik. Dochodzimy do wniosku, że program powinien informować o tym, czy podana liczba jest mniejsza, czy większa od wylosowanej. Wspólnie z uczniami dyskutujemy i zapisujemy proponowany algorytm na tablicy.
Pierwsza wersja algorytmu może wyglądać następująco: Po uruchomieniu program:
- wyświetla komunikat informujący, na czym polega gra, np.: „Pomyślałem sobie liczbę od 1 do 100. Zgadnij, co to za liczba!”
- losuje liczbę (w przedziale od 1 do 100) i zapamiętuje w zmiennej
- wyświetla napis „Podaj liczbę” i czeka na odpowiedź uczestnika gry
- porównuje odpowiedź uczestnika z wylosowaną liczbą:
- jeżeli liczba nie zgadza się
- sprawdza, czy liczba podana przez uczestnika zabawy jest większa od wylosowanej
- jeśli tak
- wyświetla napis: „Za dużo!".
- w przeciwnym przypadku
- wyświetla napis „Za mało!”
- jeśli tak
- ponownie wyświetla pytanie uczestnikowi gry, czeka na odpowiedź i porównuje ją z wylosowaną liczbą
- sprawdza, czy liczba podana przez uczestnika zabawy jest większa od wylosowanej
- jeżeli liczba zgadza się
- wyświetla napis „Brawo!”
- kończy wykonywanie skryptu
- jeżeli liczba nie zgadza się
Po rozpisaniu pierwszej wersji algorytmu zwracamy uwagę, że mamy do czynienia z pewnymi czynnościami, które będą powtarzane.
Zadajemy pytanie: Które z czynności są powtarzane? Czy wiemy ile razy? Czy umiemy sformułować warunek, jaki musi być spełniony, żeby zakończyć powtarzanie? W razie potrzeby naprowadzamy uczniów na to, że od punktu „program porównuje odpowiedź uczestnika” czynności są powtarzane tak długo, aż udzielona odpowiedź będzie prawidłowa (podana liczba zgadza się z liczbą wylosowaną przez program). Zauważamy więc, że właściwe będzie użycie odpowiedniej pętli.
Zadajemy pytanie: Która pętla się tutaj sprawdzi i co powinna objąć? Prosimy, by odnaleźli klocek pętli najlepiej pasujący ich zdaniem. W tym przypadku naprowadzamy uczniów na pętlę powtarzaj, aż.
Odpowiednio modyfikujemy zapis algorytmu na tablicy, uwzględniając w nim pętle powtarzaj, aż. Zmodyfikowany algorytm może wyglądać następująco:
Po uruchomieniu program:
- wyświetla komunikat informujący, na czym polega gra, np.: „Pomyślałem sobie liczbę od 1 do 100. Zgadnij, co to za liczba!”
- losuje liczbę (w przedziale od 1 do 100) i zapamiętuje w zmiennej
- wyświetla napis „Podaj liczbę” i czeka na odpowiedź uczestnika gry
- powtarza poniższe instrukcje tak długo, aż podana odpowiedź uczestnika jest równa wylosowanej liczbie zapamiętanej w zmiennej:
- sprawdza, czy liczba podana przez uczestnika zabawy jest większa od wylosowanej
- jeśli tak
- wyświetla napis: „Za dużo!”
- w przeciwnym przypadku
- wyświetla napis „Za mało!”
- jeśli tak
- wyświetla napis „Podaj liczbę” i czeka na odpowiedź uczestnika gry
- sprawdza, czy liczba podana przez uczestnika zabawy jest większa od wylosowanej
- wyświetla napis „Brawo!”
- kończy wykonywanie skryptu
Implementacja gry logicznej „Zgadywanie liczby”
Czas na realizację tej części: ok. 25 - 30 minut
Zadajemy pytanie uczniom: Jakiego klocka możemy użyć do zadania pytania? Gdzie zostanie zapisana odpowiedź. Prosimy, by taki klocek odnaleźli.
Uczniowie powinni odnaleźć dwa klocki, znajdujące się wśród czujników, a umieszczone jeden pod drugim.
Zadajemy pytanie uczniom: Jakich klocków możemy użyć do porównania dwóch wartości liczb. Prosimy, by taki klocek odnaleźli. Następnie pytamy, co dokładnie będziemy porównywali.
Uczniowie powinni odnaleźć klocek porównania oraz wpaść na pomysł, że porównujemy wylosowaną wartość zapisaną w zmiennej ze zmienną o nazwie odpowiedź, do której trafi wartość wpisana przez gracza. Zwracamy uczniom uwagę na konieczność utworzenia zmiennej (np. o nazwie liczba), na której będziemy pamiętać wylosowaną liczbę.
Zwracamy również uczniom uwagę, że mają do dyspozycji także klocki pozwalające sprawdzić, która liczba jest większa, co będzie przydatne podczas tworzenia skryptu gry.
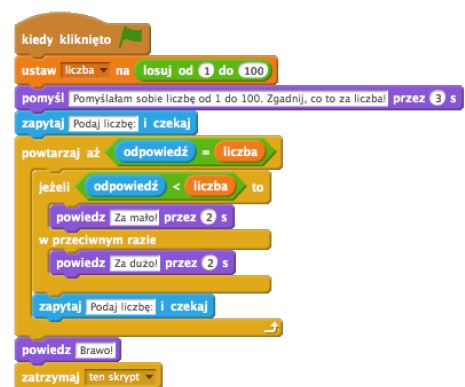
Zadanie: Prosimy, by uczniowie utworzyli skrypt według ułożonego algorytmu oraz wybrali odpowiednie tło do gry i postać duszka, który będzie komunikował się z graczem.
Przykładowy skrypt może wyglądać w następujący sposób:
Warto zwrócić uwagę uczniom (jeśli sami nie zauważą), że polecenia wyświetlające komunikaty powinny być widoczne przez określony czas (np. 2 lub 3 sekundy), a nie znikać od razu.
Przykładowa scena i duszek do gry:
Po napisaniu przez uczniów skryptu gry prosimy, by chwilę w nią pograli. Następnie prosimy, by zaproponowali sposób zadawania pytań (czyli algorytm zgadywania liczby), żeby jak najszybciej (w jak najmniejszej liczbie pytań) odgadnąć wylosowaną przez komputer liczbę.
Wprowadzenie drugiego duszka do gry i komunikacji między ich skryptami
Czas na realizację tej części: ok. 25 - 30 minut
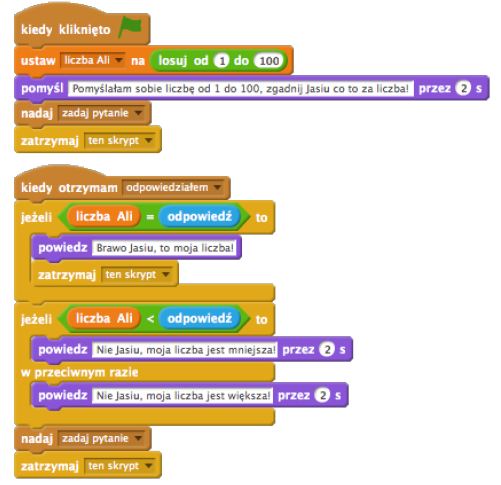
Proponujemy, by uatrakcyjnić grę poprzez wprowadzenie drugiej postaci – duszka. Wspólnie z uczniami zastanawiamy się, jak należałoby zmodyfikować nasz skrypt, by jeden duszek zadawał pytania, a drugi odpowiadał. Wnioski zapisujemy na tablicy, na przykład w postaci rysunku podobnego do poniższego.
Skrypty Ali i Jasia mogą wyglądać następująco:
Skrypt Jasia:
Przykładowa scena do zmodyfikowanego projektu:
Wprowadzenie licznika pytań
Czas na realizację tej części: ok. 10 minut
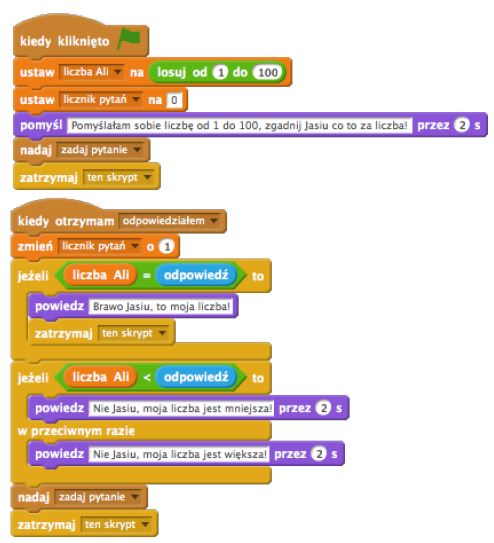
Wspólnie z uczniami zastanawiamy się, że w naszej grze brakuje jakiegoś systemu punktacji. Proponujemy, aby uczniowie w związku z tym wprowadzali zmienną licznik, która będzie zliczała, po ilu pytaniach udało się Jasiowi odgadnąć wylosowaną liczbę.
Zadanie: Prosimy, by uczniowie wprowadzili odpowiednie modyfikacje do programu samodzielnie, a później pochwalili się rozwiązaniem.
Jedno z możliwych rozwiązań:
Propozycja zadania dodatkowego do samodzielnej realizacji przez uczniów
Jako dodatkowe zadanie można zaproponować:
Program losujący dwie liczby, a następnie wyświetlający działania arytmetyczne (dodawanie, odejmowanie, mnożenie czy dzielenie) i sprawdzający poprawność udzielonej przez gracza odpowiedzi.