Scenariusz 4 - Doprowadź do celu-ćwiczymy liczenie
Materiały stworzone przez Iwonę Cugier w ramach programu Mistrzowie Kodowania, objęte licencją CC BY 3.0 PL "Creative Commons Uznanie Autorstwa 3.0 Polska".
Założenia projektu: Celem zajęć jest stworzenie kod-planu, czyli ustalenie drogi, jaką ma pokonać robot, aby dojść do określonego celu, spełniając podane warunki (zabawa liczbami). Kształcimy naukę logicznego myślenia, orientację przestrzenną, kierunki (pionowo-poziomo), spostrzegawczość, a przy okazji utrwalamy liczby i ćwiczymy liczenie, porównywanie, rozkład na składniki, itd.
Opis zajęć: Zajęcia z wykorzystaniem robota polegają na programowaniu ruchu robota, który ma dotrzeć do określonego celu, z uwzględnieniem warunków, które dotyczą rozkładania liczb na składniki, wyznaczania czynników, itp.
Wyjaśnienie celu zajęć, rozłożenie liczb.
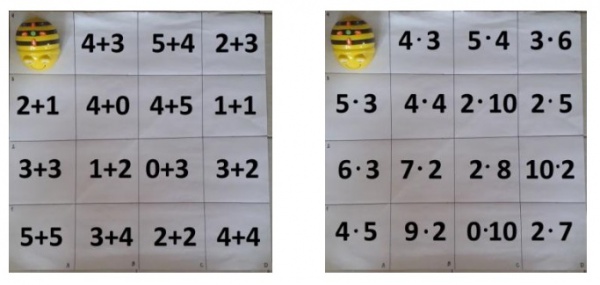
Nauczycielka prosi chętne dziecko o zabranie kartonika z określoną liczbą i położenie go na wybranym polu np. 2C. Powtarza polecenie dla następnych liczb.
Tworzenie drogi pszczółki za pomocą strzałek (praca indywidualna).
Prosimy o dotarcie do odpowiedniej liczby. Meta (określona liczba) może być wylosowana za pomocą kostki lub dwóch kostek, w zależności od zakresu liczbowego. W przypadku większych liczb dodajemy wylosowane „oczka”. Dzieci rysują możliwe warianty drogi.
Testowanie rozwiązań (praca zbiorowa).
Dzieci proponują „swoje” kody. Chętne lub wylosowane (np. za pomocą patyczków z imieniem) dziecko wprowadza „dyktowany” kod.
Warianty zabawy:
- Pszczółka ma zatrzymywać się na polach z liczbami parzystymi (nieparzystymi)
- Po wylosowaniu liczby z określonego zakresu pszczółka ma zatrzymać się na polach, na których znajdują się składniki tej liczby (czynniki dające tę liczbę)
- Po wylosowaniu działania z określonego zakresu pszczółka ma zatrzymać się na polu z wynikiem
- Po wylosowaniu liczby z określonego zakresu pszczółka ma zatrzymać się na polach, na których znajdują się znajduje się liczba większa (mniejsza).
- Pszczółka wędruje według określonego ciągu liczbowego np. od 0 do 10 (od 10 do 0), zatrzymując się na poszczególnych polach
- Pszczółka wędruje „zaliczając” wielokrotności liczby

|
W przypadku matematyki możliwości zabawy z pszczółką są nieograniczone. Można przygotować matę o większej ilości pól, przeróżne kartoniki z działaniami, z liczbami. |
UWAGA: zdjęcia ze scenariusza przedstawiają prototyp maty. Po rozłożeniu kartoników nakrywa się ją specjalną folią.